Cayley公式是说,一个完全图K_n有n^(n-2)棵生成树,换句话说n个节点的带标号的无根树有n^(n-2)个。今天我学到了Cayley公式的一个非常简单的证明,证明依赖于Prüfer编码,它是对带标号无根树的一种编码方式。
给定一棵带标号的无根树,找出编号最小的叶子节点,写下与它相邻的节点的编号,然后删掉这个叶子节点。反复执行这个操作直到只剩两个节点为止。由 于节点数n>2的树总存在叶子节点,因此一棵n个节点的无根树唯一地对应了一个长度为n-2的数列,数列中的每个数都在1到n的范围内。下面我们只 需要说明,任何一个长为n-2、取值范围在1到n之间的数列都唯一地对应了一棵n个节点的无根树,这样我们的带标号无根树就和Prüfer编码之间形成一 一对应的关系,Cayley公式便不证自明了。
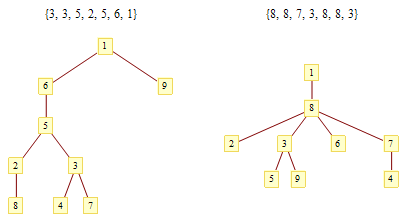
注意到,如果一个节点A不是叶子节点,那么它至少有两条边;但在上述过程结束后,整个图只剩下一条边,因此节点A的至少一个相邻节点被去掉过,节 点A的编号将会在这棵树对应的Prüfer编码中出现。反过来,在Prüfer编码中出现过的数字显然不可能是这棵树(初始时)的叶子。于是我们看到,没 有在Prüfer编码中出现过的数字恰好就是这棵树(初始时)的叶子节点。找出没有出现过的数字中最小的那一个(比如④),它就是与Prüfer编码中第 一个数所标识的节点(比如③)相邻的叶子。接下来,我们递归地考虑后面n-3位编码(别忘了编码总长是n-2):找出除④以外不在后n-3位编码中的最小 的数(左图的例子中是⑦),将它连接到整个编码的第2个数所对应的节点上(例子中还是③)。再接下来,找出除④和⑦以外后n-4位编码中最小的不被包含的 数,做同样的处理……依次把③⑧②⑤⑥与编码中第3、4、5、6、7位所表示的节点相连。最后,我们还有①和⑨没处理过,直接把它们俩连接起来就行了。由 于没处理过的节点数总比剩下的编码长度大2,因此我们总能找到一个最小的没在剩余编码中出现的数,算法总能进行下去。这样,任何一个Prüfer编码都唯 一地对应了一棵无根树,有多少个n-2位的Prüfer编码就有多少个带标号的无根树。
一个有趣的推广是,n个节点的度依次为D1, D2, ..., Dn的无根树共有(n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]个,因为此时Prüfer编码中的数字i恰好出现Di-1次。

